

![]()
|
|
|
Home Contact us About us Iran highlights Guides |

Iran (Persian) Calendar
A solar calendar with years of 365 days each was in use in pre-Islamic Persia already. Every year consisted of 12 months with 30 days each, and five additional days. These additional days were being inserted between the 8th and the 9th month. From the year 1000 or so on, the extra days were shifted to the end of the year. With the tropical year 0,2422 days longer than the old Persian year, the beginning of the calendar year moved backwards a day every four years. Soon, taxes had to be paid before harvesting, which was simply impossible. Therefore, caliph al-Mutawakkil (r. 847-861) proposed to delay New Year, called Naw Ruz, by 57 days, but the reform seems not to have been carried out. Caliph al-Mu'tadid (r. 892-902) ordered Naw Ruz to be delayed by 60 days, but this reform, too, didn't come into effect. In 1079, the Selchuk Djalal ad-Din Malik Shah fixed Naw Ruz to the vernal equinox. The year should have 365 days until the sun didn't enter Aries before noon on the last day of the year. In this case, six additional days had to be counted. There was no regular leap year pattern, despite the proposal of a leap year cycle of 33 years, containing 8 leap years, by the mathematician, astronomer, and poet Omar Khayyam. With this rule, the Persian year would have had a mean length of 3658/33 = 365.2424.. days, which would even be more accurate than the Gregorian year. The modern Persian calendar uses quite complicated leap year rules, defining a 2820-year cycle with 683 leap years, which results a in mean length of a year of 365683/2820 = 365,2422 days. Considering the length of the tropical year as being constant, the remaining error would amount to a day in more than 2 million years! The 2820-year cycle is divided into 21 sub cycles of 128 years each, and a 132-year sub cycle at the end of each 2820-year cycle. A 128-year sub cycle consists of a 29-year sub-sub cycle, followed by 3 sub-sub cycles of 33 years each. Finally, the 132-year sub cycle consists of one sub-sub cycle of 29 years, followed by two 33-year sub-sub cycles and a final sub-sub cycle of 37 years. The years are numbered within each cycle. Writing n for the number of a year within a cycle, this year is a leap year if n > 1 and n mod 4 = 1. A year of the Persian calendar has 12 months, the order, names, and lengths of which can be seen in the following table (* - length of the month in leap years).
The years are counted from the year 622 CE on, which was the year of the Hidjra, Mohammed's escape from Mekkah to Medina. Thus, on 21 March 2001, the Persian year 1380 began with 1 Farvardin. The Persian year 1381 began on 21 March 2002, Gregorian. Table for the Conversion of Persian Dates into Gregorian DatesThe table mainly consists of three columns in which the Gregorian dates of the first day of each Persian month are given for the several possibilities of Gregorian and Persian normal and leap years falling on each other. The difference between the Gregorian and Persian number of the year is shown in the last column, that difference being 621 for the months from Farvardin to Dey and 622 for the last two months of the Persian year, Bahman and Esfand. To convert a Persian date into a Gregorian one first find the column in which the Persian number of the year is to be found. On top of that column find the Gregorian date of the first day of the Persian month which the date to be converted is in. Increase the year number by the number shown in the last column of the row of the Persian month. ExampleWhat is the Gregorian date of 10 Tir 1369 (Persian)? The number 1369 is to be found in the middle column of the table. In the upper part of that column we find 1 Tir = 22 June. The number of the Gregorian year is 1369 + 621 = 1990. Thus, 1 Tir 1369 (Persian) corresponds to 22 June 1990 (Gregorian). Going nine days ahead we find 10 Tir 1369 on 31 June 1990 which is 1 July 1990, because June has only 30 days.
|
 |
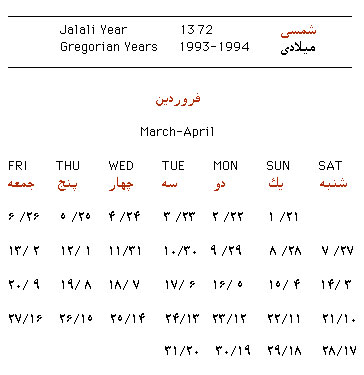 The calendar in use in Iran and Afghanistan today was introduced in Persia in
1925, while Afghanistan adopted the calendar in 1957, using the Arab names of
the zodiacal signs for the corresponding months of the Persian calendar.
The calendar in use in Iran and Afghanistan today was introduced in Persia in
1925, while Afghanistan adopted the calendar in 1957, using the Arab names of
the zodiacal signs for the corresponding months of the Persian calendar.